Author(s)
| Name | Institution | Mail Address | Social Contacts |
|---|---|---|---|
| Leonardo Giannini | INFN Sezione di Pisa / UCSD | leonardo.giannini@cern.ch | |
| Tommaso Boccali | INFN Sezione di Pisa | tommaso.boccali@pi.infn.it | Skype: tomboc73; Hangouts: tommaso.boccali@gmail.com |
How to Obtain Support
| tommaso.boccali@pi.infn.it, leonardo.giannini@cern.ch | |
| Social | Skype: tomboc73 |
| Jira |
General Information
| ML/DL Technologies | LSTM, CNN |
|---|---|
| Science Fields | High Energy Physics |
| Difficulty | Low |
| Language | English |
| Type | fully annotated and runnable |
Software and Tools
| Programming Language | Python |
|---|---|
| ML Toolset | Keras + Tensorflow |
| Additional libraries | uproot |
| Suggested Environments | INFN-Cloud VM, bare Linux Node, Google CoLab |
Needed datasets
| Data Creator | CMS Experiment |
|---|---|
| Data Type | Simulation |
| Data Size | 1 GB |
| Data Source | INFN Pandora |
Short Description of the Use Case
Jets originating form b quarks have peculiar characteristics that one can exploit to discriminate them from jets originating from light quarks and gluons, and to better reconstruct their momentum. Both tasks have been dealt with using ML and are now tackled with Deep Learning techniques.
Two original Deep Learning applications, both involving b quark jets, are described in this chapter.
The first application described is the momentum regression, the second one is b-tagging algorithm which aims at processing lower level data, and lets a DNN learn the secondary vertex information.
A combination of this tagger, called "DeepVertex", with another state-of-the-art tagger, called "DeepJet", which aims at a single particle and secondary vertex description of the jet, is also presented.
Both the regression and the DeepVertex tagger improve on the previously developed benchmark algorithms applied in Physics Analysis by the CMS collaboration.
Furthermore, the combination of "DeepVertex" and "DeepJet" reaches unprecedented performance in simulation.
The DNN regression was developed together with ETH collaborators working on the search for Higgs pairs, but was deployed in data specifically for the VH(b \bar b) analysis. The DeepJet algorithm was developed in parallel to DeepVertex by other groups, while DeepVertex and the combinations are presented in the thesis for the first time.
This hands on is largely inherited from an Hands-on by Leonardo Giannini (CMS / UCSD / formerly INFN Pisa) for the Scientific Data Analysis School at Scuola Normale, November 2019.
A complete explanation of the tutorial is available for download here (alternate URL here).
How to execute it
Way #1: Use Googe Colab
Google's Colaboratory (https://colab.research.google.com/) is tool offered by Google which offers a Jupyter like environment on a Google hosted machine, with some added features, like the possibility to attach a GPU or a TPU if needed.
You can access directly Colab by clicking on a .ipynb (Python Notebook) file. The notebooks for this tutorial can be found here. The .ipynb files are also available in the next attachment.
drive-download-20200317T155726Z-001.zip
(testnew here)
The input files are on Google Drive, and are automatically loaded by the notebooks. In case, they are also available here and here.
In the following the most important excerpts are described.
Way #2: Use Python from a ML-INFN Virtual machine
Another option is to use not Colab, but a real VM as made available by ML-INFN (LINK MISSING), or any properly configured host.
In that case, you can run the python code from the following link. You will also need to provide the input files here and here.
The tar file, to be unpacked via
tar zxvf btagging_cms.tar.gz
contains 5 python scripts with the same name as the notebooks. It can be downloaded on the virtual machine via
wget https://confluence.infn.it/download/attachments/33161478/btagging_cms.tar.gz
The 2 input files can be downloaded as
davix-get https://pandora.infn.it/public/307caa/dl/test93_0_20000.npz test93_0_20000.npz
davix-get https://pandora.infn.it/public/ec5e6a/dl/test93_20000_40000.npz test93_20000_40000.npz
Way #3: Use Jupyter notebooks from a ML-INFN Virtual machine
This way is somehow intermediate between #1 and #2. It still uses a browser environment and a Jupyter notebook, but the processing engine is on a ML-INFN instead of Google's public cloud.
You can get access to a Jupyter environment from XXX (same machine as #2), but insted from logging on that via ssh, you connect to hestname:888 and provide the password you selected at creation time. At than point, you can upload the .ipynb notebooks from drive-download-20200317T155726Z-001.zip (alternate URL here).
Annotated Description
What is (jet) b-tagging?
It is the identification (or "tagging") of jets originating from bottom quark.
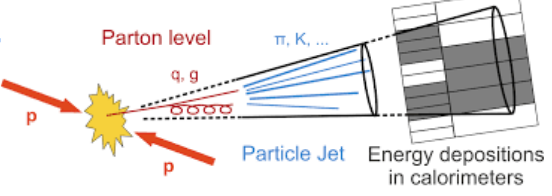
- So what is a jet?
- A collection of collimated particles originating from the hadronization of a quark or a gluon
- Clustering particles and detector signal in jets is the way we reconstruct the originating partons
- Why b-jet tagging?
- Jets production is one of the most common processes at the LHC and a background for many analyses
- b-jets production is suppressed compared to light quark/gluon jets
- Final states with b-jets are interesting for many analyses:
- Top quark
- H-> bb
- HH (bb+XX)
- etc.
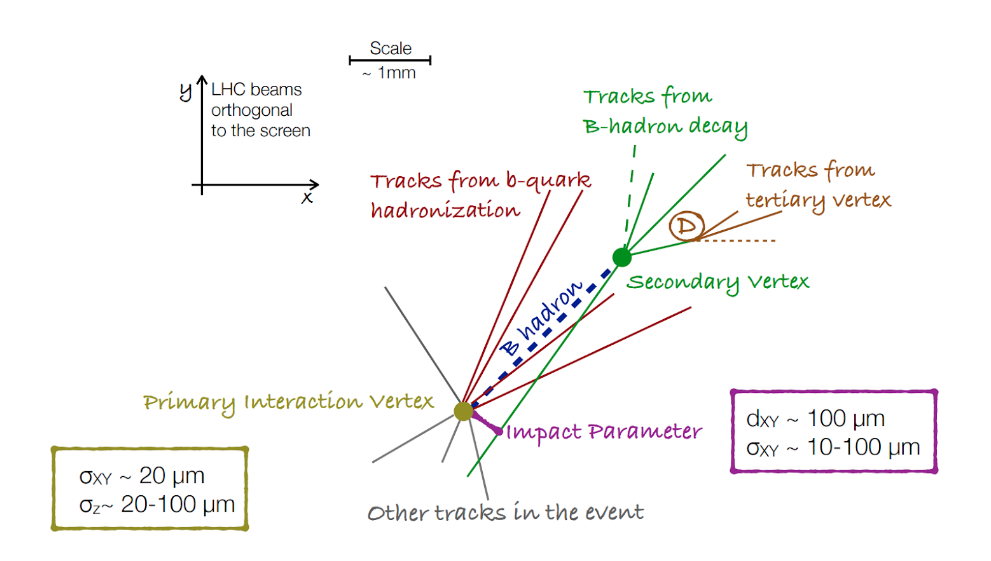
The so-called b-jets (coming from the hadronization of b quarks) have characteristics like:
- sizeable lifetime (cτ ~ 500 μm) → decay length of a few mm when boosted
- Significant Impact Parameter (IP)
- Secondary vertex
- Large mass (5 GeV)
- High rate of semileptonic decays (25%)
- High momentum transfer to the B hadron
b-tagging relies mostly on the reconstruction of the B hadrons decay products:
- Efficient and robust tracking needed
- Displaced tracks
- with good IP resolution
- Secondary vertex reconstruction
Typical b-tagging algorithms @ CMS
They
- Can use single discriminating variables
- Tracks IP, Secondary vertices
- Can combine several discriminating variables with ML
- ML is used to combine the information in an optimal way → better performance
- ML techniques are also more robust under different conditions (pileup, tracker detector, tracking etc.)
- With Deep Learning we can also bypass some of the choices we make before optimization
- using lower level inputs
- It can be more flexible and ultimately better performing
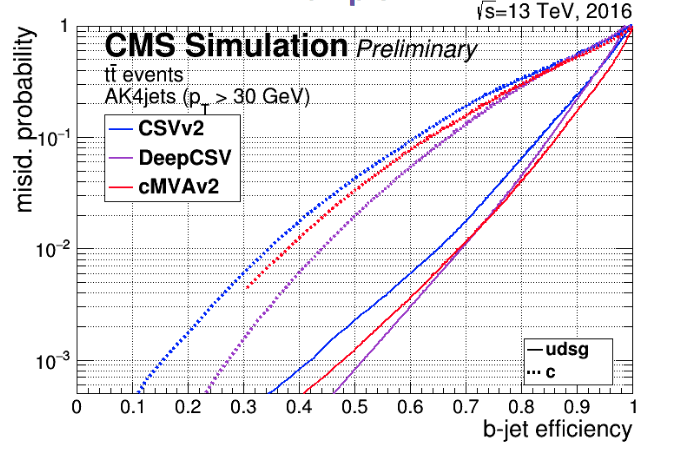
Algorithmic performance is usually described in the form of ROC (Receiver Operating Characteristics) which has on one axis (x) the efficiency in correctly tagging the signal (b-jets), and on the (y) axis the fraction of non signal jets incorrectly flagged as signal. In the b-tagging studies, unless specified otherwise, "non signal jets" are defined as those coming from the hadronization of light quarks (uds) and gluons.
Jets from c quarks, which have intermediate values of lifetime with respect to b quarks, are usually treated in a separate way.
In this illustration form, an algorithm is better if the ROC curve is closer to the lower right corner of the picture
The current best performing algorithm in CMS is DeepCSV, which uses in input variables like:
- 3 categories: vertex - no vertex - pseudovertex depending on the reconstruction of a secondary decay vertex;
- ~ 20 “tagging variables”, among which the parameters of a track subset, the presence of secondary vertices and leptons.
A new b-tagging algorithm
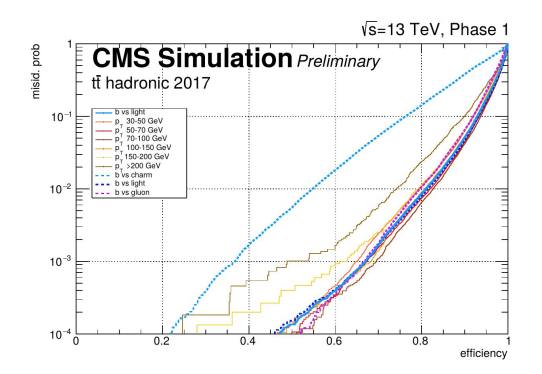
The rest of the tutorial focuses on the development of a "toy but realistic DNN algorithm", which includes vertexing, instead of having vertexing results as pre-computed input. Its inputs is, thus, mostly tracks. The real system, used by CMS, has better performance than the DeepCSV, with a (preliminary) ROC
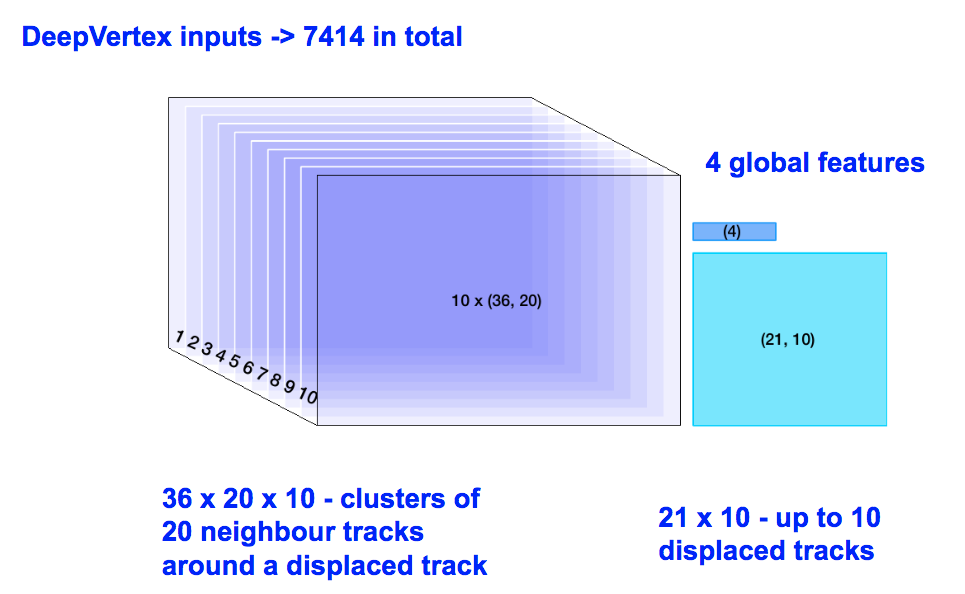
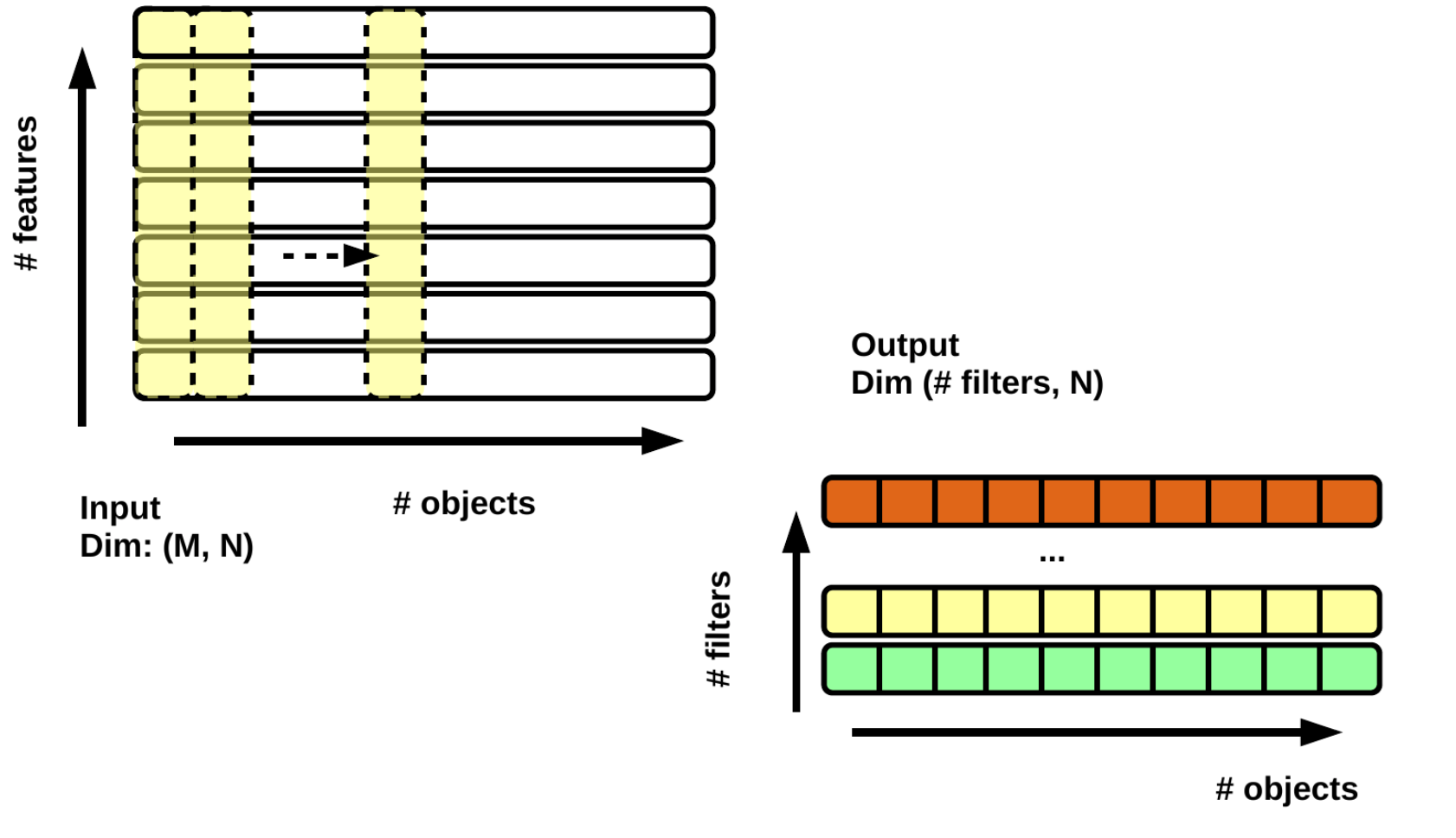
In its architecture, 7414 inputs are used, mostly coming from clusters of neighbouring tracks around a 'seed" displaced track. 10 such displaced tracks are considered at most, and 20 neighbouring tracks are in input for each of these. Each of the tracks is described via 36 parameters. On top on that, a few global quantities are added. The parameter count is explicit in the next figure
Long-Short term memories (LSTM) are used in order to reduce the parameter count, since there is no reason to believe that any of the 20 tracks per "seed" should be treated differently. After the application of the LSTM, convolutional filters and dense layers are used to are used scale to 4 output classes ("b","c", "uds", "gluon").
The tutorial
The tutorial includes 5 Jupyter Notebooks, which can be run under Google's Colab. In order to be able and run and modify files, please use the link "Open in playground" as in the picture below, or generate a private copy of the notebook from the File menu.
Notebook #1: plot_NNinput.ipynb
This notebook loads a file containing precomputed features from MC events (from CMS), including reconstructed features and Monte Carlo Truth.
It contains 6 sets of variables, the first set "arr_0" being explicitly
f["arr_0"]
shape (20000, 52)
data relative to 20000 jets
- 52 variables per jet
Ntuple content kinematics
0. "jet_pt"
1. "jet_eta"
# of particles / vertices
2. "nCpfcand"
3. "nNpfcand",
4. "nsv",
5. "npv",
6. "n_seeds",
b tagging discriminataing variables
7. "TagVarCSV_trackSumJetEtRatio"
8. "TagVarCSV_trackSumJetDeltaR",
9. "TagVarCSV_vertexCategory",
10. "TagVarCSV_trackSip2dValAboveCharm",
11. "TagVarCSV_trackSip2dSigAboveCharm",
12. "TagVarCSV_trackSip3dValAboveCharm",
13. "TagVarCSV_trackSip3dSigAboveCharm",
14. "TagVarCSV_jetNSelectedTracks",
15. "TagVarCSV_jetNTracksEtaRel",
other kinematics
16. "jet_corr_pt",
17. "jet_phi",
18. "jet_mass",
19. detailed truth
19. "isB",
20. "isGBB",
21. "isBB",
22. "isLeptonicB",
23. "isLeptonicB_C",
24. "isC",
25. "isGCC",
26. "isCC",
27. "isUD",
28. "isS",
29. "isG",
30. "isUndefined",
31. "isPhysB",
32. "isPhysGBB",
33. "isPhysBB",
34. "isPhysLeptonicB",
35. "isPhysLeptonicB_C",
36. "isPhysC",
37. "isPhysGCC",
38. "isPhysCC",
39. "isPhysUD",
40. "isPhysS",
41. "isPhysG",
42. "isPhysUndefined"
truth (6 categories)
43. "isB*1",
44. "isBB+isGBB",
45. "isLeptonicB+isLeptonicB_C",
46. "isC+isGCC+isCC",
47. "isUD+isS",
48. "isG*1",
49. "isUndefined*1",
truth as integer (used in the notebook)
50. "5x(isB+isBB+isGBB+isLeptonicB+isLeptonicB_C)+4x(isC+isGCC+isCC)+1x(isUD+isS)+21xisG+0xisUndefined",
alternative definition
51. "5x(isPhysB+isPhysBB+isPhysGBB+isPhysLeptonicB+isPhysLeptonicB_C)+4x(isPhysC+isPhysGCC+isPhysCC)+1x(isPhysUD+isPhysS)+21xisPhysG+0xisPhysUndefined"
In particular, arr_0[:-2] (the "truth as integer" above) can be used as the "Monte Carlo" category.
You are shown how to make plots of the quantities per signal and background via the definition of the function
plotter_wbins, which uses the category definition
isB=jetvars[:,-2]==5
isC=jetvars[:,-2]==4
isL=jetvars[:,-2]==1
isG=jetvars[:,-2]==21
categories=[isB, isC, isL, isG]
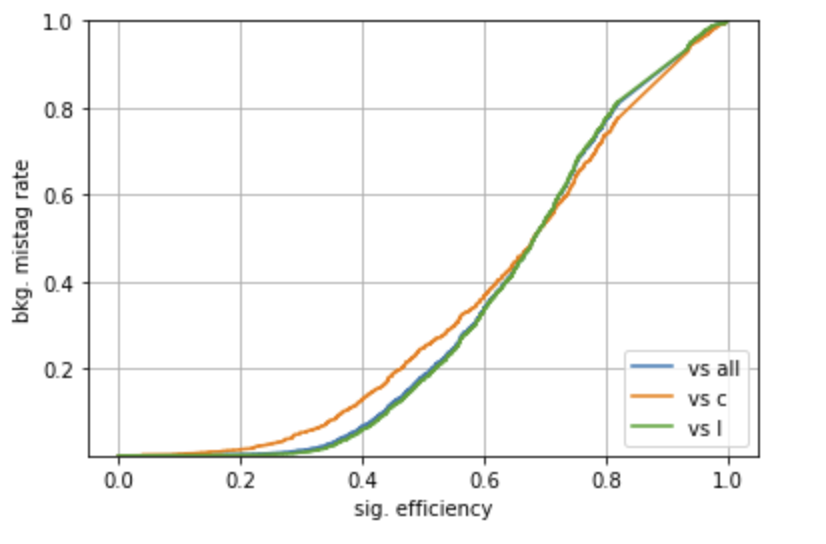
Plotting a ROC
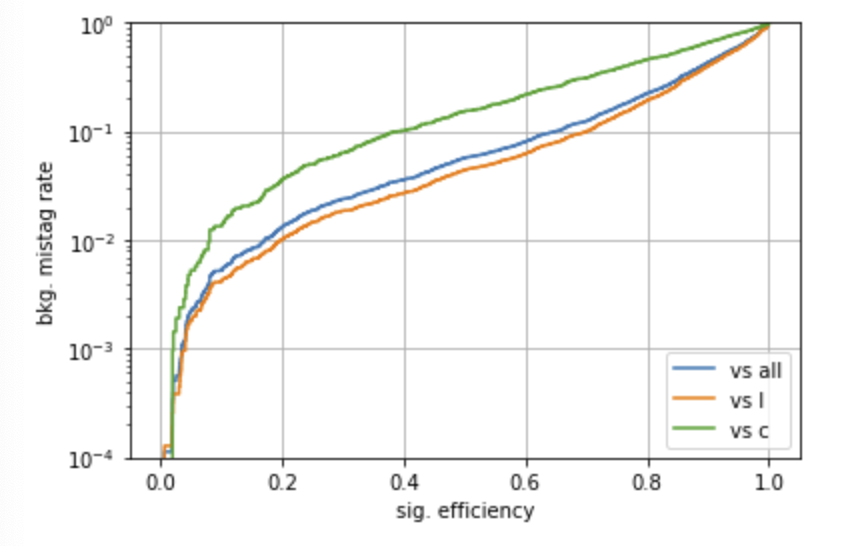
A ROC curve can be constructed, using a scan on a specific input (use TagVarCSV_trackSip2dSigAboveCharm here), with the code
from sklearn.metrics import roc_curve, auc
# b vs light and gluon roc curve
# B vs other categories -> we use isB
isBvsC = isB[isB+isC]
isBvsUSDG = isB[isB+isL+isG]
# B vs ALL roc curve
fpr, tpr, threshold = roc_curve(isB,jetvars[:,11])
auc1 = auc(fpr, tpr)
# B vs c
fpr2, tpr2, threshold = roc_curve(isBvsC,jetvars[:,11][isB+isC])
auc2 = auc(fpr2, tpr2)
# B vs light/gluon
fpr3, tpr3, threshold = roc_curve(isBvsUSDG, jetvars[:,11][isB+isL+isG])
auc3 = auc(fpr3, tpr3)
# print AUC
print (auc1, auc2, auc3)
pyplot.plot(tpr,fpr,label="vs all")
pyplot.plot(tpr2,fpr2,label="vs c")
pyplot.plot(tpr3,fpr3,label="vs l")
pyplot.xlabel("sig. efficiency")
pyplot.ylabel("bkg. mistag rate")
pyplot.ylim(0.000001,1)
pyplot.grid(True)
pyplot.legend(loc='lower right')
Notebook #2: plot_seedingTrackFeatures.ipynb
It is very similar to previous example, but looks into the other ntuples in the file, which we did not consider before
print(f["arr_0"].shape)
print(f["arr_1"].shape)
print(f["arr_2"].shape)
print(f["arr_3"].shape)
print(f["arr_4"].shape)
print(f["arr_5"].shape)
gives
(20000, 52)
(20000, 10, 21)
(20000, 25, 6)
(20000, 25, 16)
(20000, 4, 12)
(20000, 720, 10)
We already saw the first one, with 52 "features". The others have
10x21 -> (max) 10 tracks with impact parameter > 1 sigma : 21 variabili per track associated to the jet
16x25 -> (max) 16 charged particles : 25 variables each
6x25 -> (max) 6 neutral particles : 25 variables each
4x12 -> (max )4 secondary vertices associated to the jet : 12 variables each
720x10 -> low level information used in input to the DNN - foe arch of the (max 10) tracks with high impact parameter, consider the 20 closest tracks FIX.You can go on studying these features.
Notebook #3: keras_DNN.ipynb
This notebook trains a Dense network using the input features described in the previous sections.
First of all, which features to use in the network are selected
dataALL=f["arr_0"]
jetInfo=dataALL[:,[0,1,2,3,4,5,7,8,9,10,11,12,13,14,15]]
with the definitions explained in the next notebooks (for example, "1" is the eta of the jet).
With these, a dense network is created:
inputLayer = Input(shape=(15,))
x = BatchNormalization()(inputLayer)
####
x = Dense(30, activation='relu')(x)
x = Dropout(rate=dropoutRate)(x)
x = Dense(30, activation='relu')(x)
x = Dropout(rate=dropoutRate)(x)
####
x = Dense(20, activation='relu')(x)
x = Dropout(rate=dropoutRate)(x)
####
x = Dense(10, activation='relu')(x)
x = Dropout(rate=dropoutRate)(x)
####
outputLayer = Dense(6, activation='softmax')(x)
####
model = Model(inputs=inputLayer, outputs=outputLayer)
where 15 is the number of input features (please note that in the list above "6" is missing!), followed by
- a normalization layer (to have uniform ranged numbners)
- Dense and Dropout layers interleaved.
Dropout layers are used in general to avoid overtraining, by dropping different nodes at each training cycle.
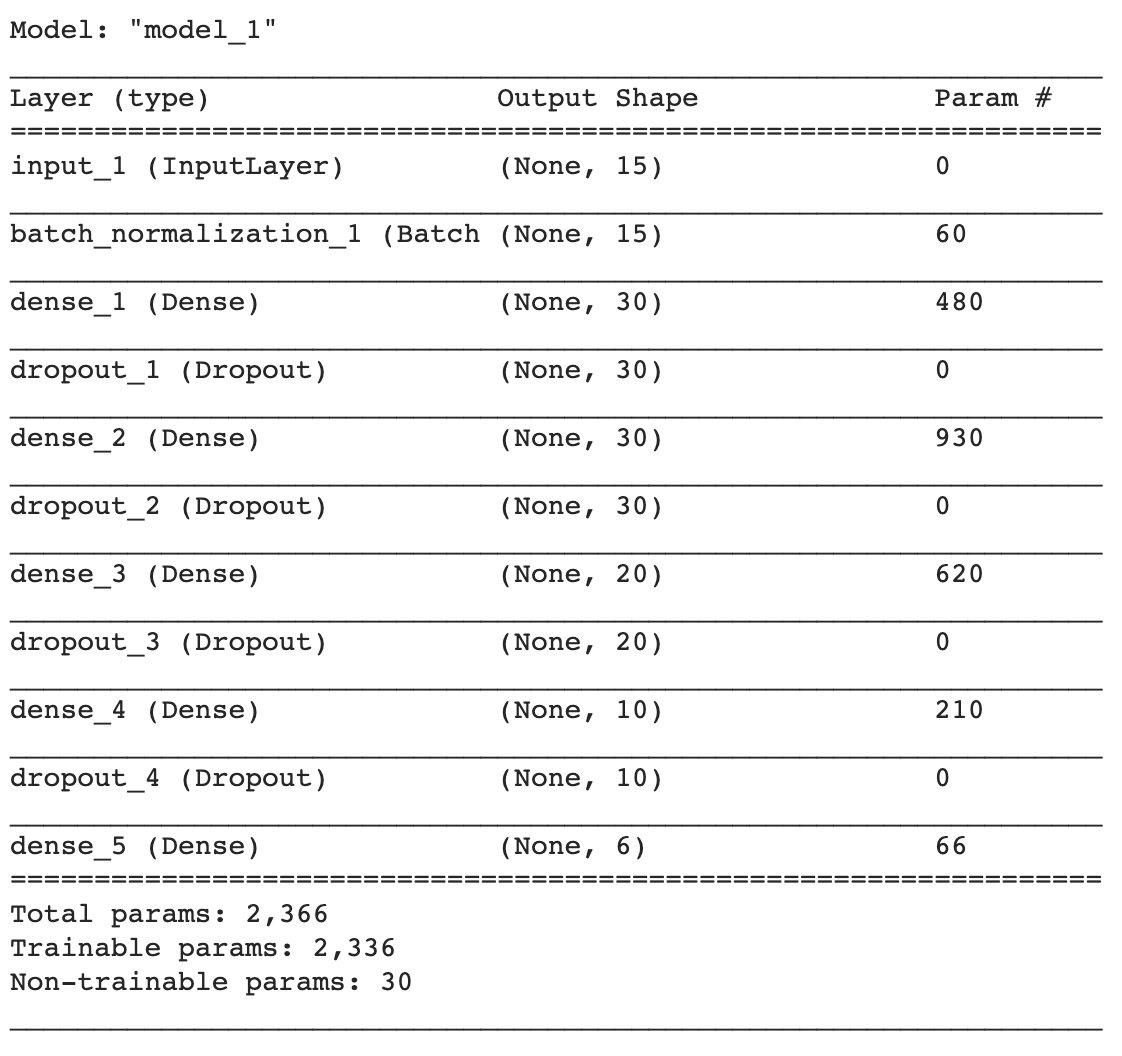
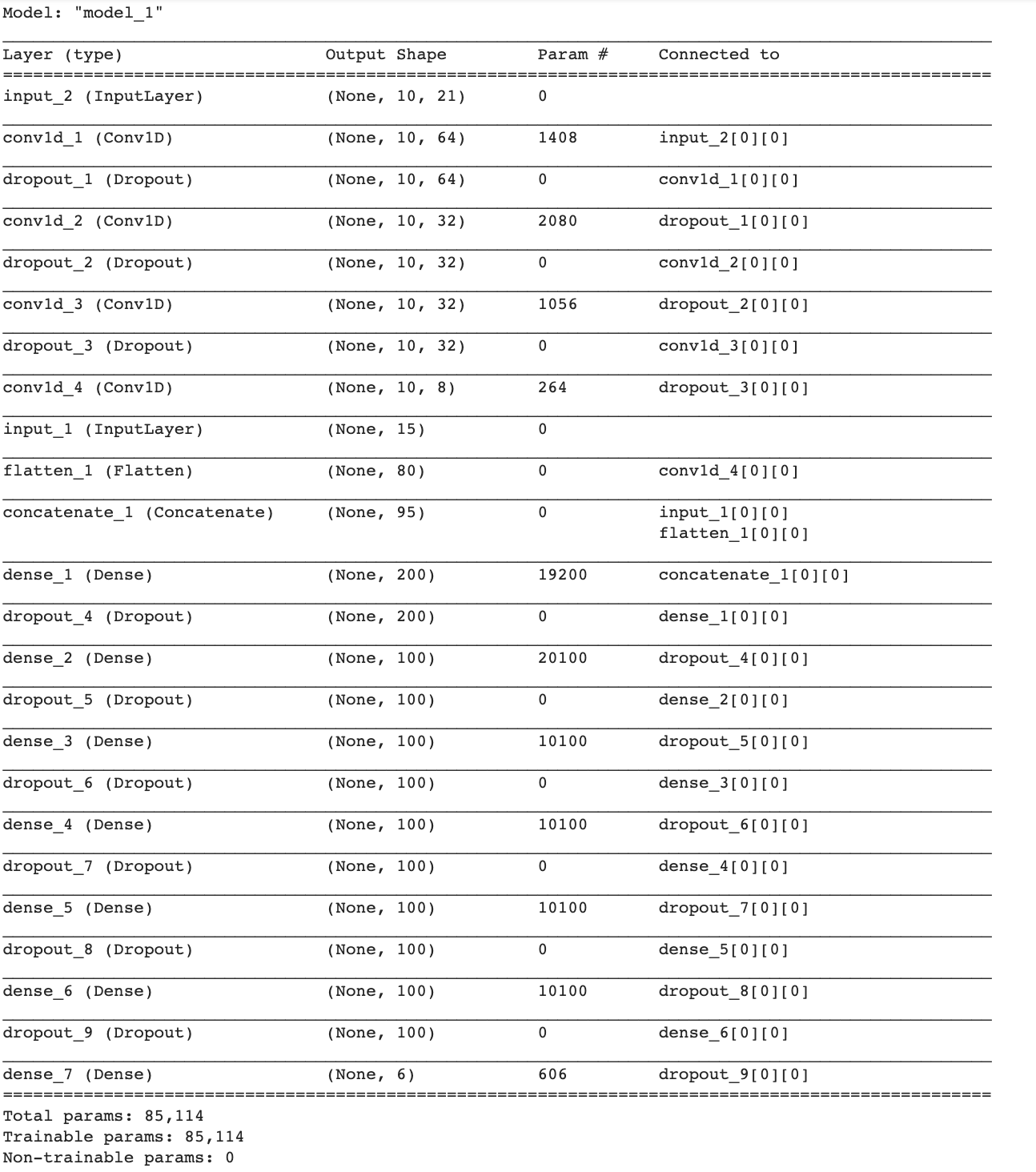
After compilation, the Deep Neural Network geometry is
Dropout layers have no parameters to train; dense layers have a number of weights scaling as [Number of nodes in the previous layer +1 (the bias)]*[Number of nodes in this layer].
For example, a a Dense layer with 30 nodes reading from a 30 nodes layer, will have (30+1)*30 = 930 parameters.
Training the model with
history = model.fit(jetInfo, jetCategories, epochs=n_epochs, batch_size=batch_size, verbose = 2,
validation_split=0.3,
callbacks = [
EarlyStopping(monitor='val_loss', patience=10, verbose=1),
ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=2, verbose=1),
TerminateOnNaN()])
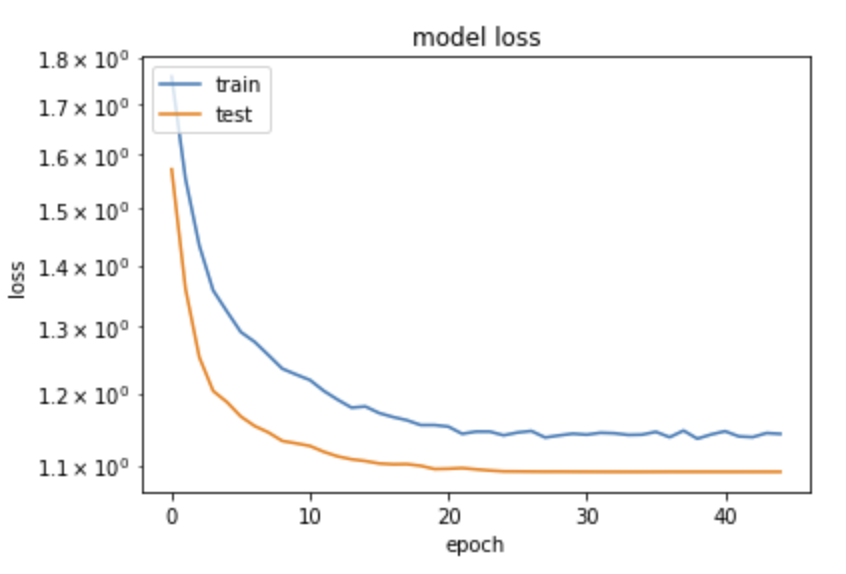
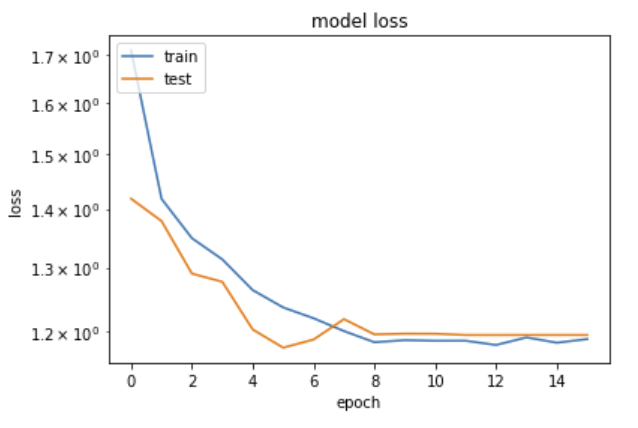
An useful view is the plot of the loss (on train and test samples) along the iterations.
from matplotlib import pyplot as plt
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.yscale('log')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
We can use the second file as a validation set, to plot, for example, ROC curves. One builds a similar shaped set out of that
test=numpy.load("test93_20000_40000.npz")
testALL=test["arr_0"]
jetInfoTEST=testALL[:,[0,1,2,3,4,5,7,8,9,10,11,12,13,14,15]]
jetCategoriesTEST=testALL[:,-9:-3]And uses the model to get a prediction
predict_test = model.predict(jetInfoTEST)
Check the notebook for the actual python, code, which results in a ROC like
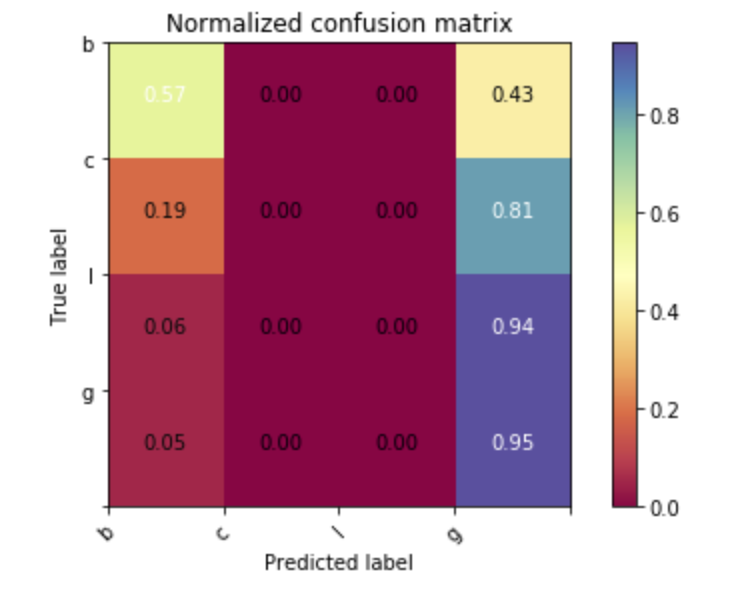
The confusion matrix defines how good is the match between predicted and true categories.
Since in the output we have less categories than in the input (output is either b or not b), it is not strictly diagonal, and upon normalization shows
Without cuts, a "b" is recognized 57% of the time as a "b" and 43% as a light. Clearly, this is low figure but depends on the cut on the output.
Notebook #4: CNN1x1_btag.ipynb
The fourth notebook builds a convolutional NN using the same input features, PLUS the single tracks features in arr_1
dataJET=f["arr_0"]
jetInfo=dataJET[:,[0,1,2,3,4,5,7,8,9,10,11,12,13,14,15]]
jetCategories=dataJET[:,-9:-3]
# Select addtional variables with more tracks from the 2nd ntuple
dataTRACKS=f["arr_1"]
# Check shape
print(jetInfo.shape, jetCategories.shape, dataTRACKS.shape)
(20000, 15) (20000, 6) (20000, 10, 21)
We start adding 1x1 convolution
You need to load from tensorflow the needed packages
# keras imports
from keras.models import Model
from keras.layers import Dense, Input, Conv2D, Dropout, Flatten, Concatenate, Reshape, BatchNormalization
from keras.layers import Conv1D
And then we can define the network
Inputs=[Input(shape=(15,)) ]
Inputs+=[Input(shape=(10,21))]
tracks=Inputs[1]
tracks = Conv1D(64, 1, kernel_initializer='lecun_uniform', activation='relu')(tracks)
tracks = Dropout(rate=dropoutRate)(tracks)
tracks = Conv1D(32, 1, kernel_initializer='lecun_uniform', activation='relu')(tracks)
tracks = Dropout(rate=dropoutRate)(tracks)
tracks = Conv1D(32, 1, kernel_initializer='lecun_uniform', activation='relu')(tracks)
tracks = Dropout(rate=dropoutRate)(tracks)
tracks = Conv1D(8, 1, kernel_initializer='lecun_uniform', activation='relu')(tracks)
tracks = Flatten()(tracks)
x = Concatenate()( [Inputs[0] , tracks] )
x= Dense(200, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
predictions = Dense(6, activation='softmax',kernel_initializer='lecun_uniform')(x)
model = Model(inputs=Inputs, outputs=predictions)
model.compile(loss='categorical_crossentropy', optimizer='adam')
model.summary()
The number of free parameters is much larger than before (85k vs 2k), due to the fact that we input larger dimensionality inputs (matrices instead of vectors).
# train
history = model.fit([jetInfo, dataTRACKS], jetCategories, epochs=n_epochs, batch_size=batch_size, verbose = 2,
validation_split=0.3,
callbacks = [
EarlyStopping(monitor='val_loss', patience=10, verbose=1),
ReduceLROnPlateau(monitor='val_loss', factor=0.1, patience=2, verbose=1),
TerminateOnNaN()])
# plot training history
from matplotlib import pyplot as plt
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.yscale('log')
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'test'], loc='upper left')
plt.show()
Using the test samples from the second file, one can produce the ROC curves and the confusion matrices as in the previous example.
Notebook #5 MLINFN-2 BACKLOG : lstm_btag.ipynb
The fifth notebook is very similar to the fourth, but uses a Long Short-Term Memory to input sequentially data instead of having a full matrix. The inputs are the same
# keras imports
from keras.models import Model
from keras.layers import Dense, Input, Conv2D, Dropout, Flatten, Concatenate, Reshape, BatchNormalization
from keras.layers import LSTM
Inputs=[Input(shape=(15,)) ]
Inputs+=[Input(shape=(10,21))]
tracks=Inputs[1]
tracks = LSTM(64)(tracks)
x = Concatenate()( [Inputs[0] , tracks] )
x= Dense(200, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
x= Dense(100, activation='relu',kernel_initializer='lecun_uniform')(x)
x = Dropout(rate=dropoutRate)(x)
predictions = Dense(6, activation='softmax',kernel_initializer='lecun_uniform')(x)
model = Model(inputs=Inputs, outputs=predictions)
In this way, "tracks" are processed one at a time. Note that an LSTM is a complex node, with many weights, hence the total number of free parameters does not necessarily decrease with respect to easier network topologies
model.compile(loss='categorical_crossentropy', optimizer='adam')
model.summary()
From this point on, the treatment of the test samples, ROC, and confusion matrices are the same as in the previous example.
References
- Slides as presented at Scientific Data Analysis School at Scuola Normale, November 2019: here.
- CMS btagging results: here.
Attachments